zpět na matematiku   zpět na život školy

Pythagorova věta, Pythagorejský trojúhelník, Pythagorejská čísla pro ZŠ

Obsah:

Pythagorova věta

Pythagorova věta popisuje vztah, který platí mezi délkami stran v pravoúhlém trojúhelníku v rovině. Umožňuje dopočítat délku třetí strany takového trojúhelníka, pokud jsou známy délky dvou zbývajících stran.

Pythagorova věta zní:




V pravoúhlém trojúhelníku platí, že
obsah čtverce sestrojeného nad přeponou je roven součtu obsahů čtverců sestrojených nad oběma odvěsnami.

Přepona je nejdelší strana a odvěsna jsou dvě kratší strany v pravoúhlém trojúhelníku.

  
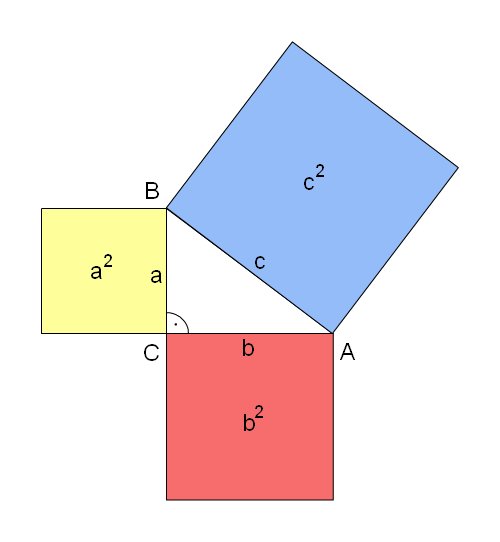
Formálně Pythagorovu větu vyjadřuje rovnice:

a2 + b2 = c2



kde
písmeno c označuje délku přepony,
písmena a a b označují délky odvěsen pravoúhlého trojúhelníku.





Rovnice pro výpočet délky přepony
c2 = a2 + b2



Rovnice pro výpočet délek odvěsen
a2 = c2 - b2
b2 = c2 - a2

Pythagorovu větu lze použít i obráceně ke zjištění, zda je daný trojúhelník pravoúhlý.

Obrácená Pythagorova věta zní:
Jestliže v trojúhelníku platí, že součet obsahů čtverců sestrojených nad kratšími stranami je roven obsahu čtverce sestrojeného nad nejdelší stranou, potom je tento trojúhelník pravoúhlý.

nahoru

Pythagorejský trojúhelník

Pythagorejský trojúhelník je pravoúhlý trojúhelník, jehož délky strany jsou vyjádřeny celými (přirozenými) čísly.
Nejznámnější pythagorejský trojúhelník má délky stran 3, 4, 5.

Pro délky stran v pravoúhlém trojúhelníku platí Pythagorova věta (viz výše),
proto musí pro trojici čísel 3, 4, 5 platit  32 + 42 = 52

Jiné trojice přirozených čísel, které jsou délkami stran pythagorejských trojúhelníků jsou např.
6, 8, 10;      8, 15, 17;      5, 12, 13;      12, 16, 20;      20, 21, 29;   apod.

Těmto trojicím přirozených čísel říkáme Pythagorejská čísla.

nahoru

Pythagorejská čísla a jejich výpočet

Pythagorejská čísla jsou tvořena trojicí přirozených čísel a, b, c, pro které platí a2 + b2 = c2. Jsou to tedy přirozená čísla vyhovující Pythagorově větě.

Pythagorejská čísla lze vytvořit podle následující věty:
Čísla a, b, c jsou pythagorejská právě tehdy, jestliže je lze vyjádřit ve tvaru a = p² - q², b = 2·p·q, c = p² + q² pro libovolná přirozená čísla p, q, pro která platí p > q. Např.

pro p = 1 a q = 2 dostaneme trojici a = 3, b = 4, c = 5,
pro p = 2 a q = 5 dostaneme trojici a = 20, b = 21, c = 29.

Výpočet Pythagorejských čísel

Tento formulář vypočítá pro dvě různá přirozená čísla p a q trojici Pythagorejských čísel.

Vlož dvě přirozená čísla: p: q:



Pythagorejská čísla:

nahoru

Historie

nahoru

Haperdonapté – napínači lan ve starověkém Egyptě

   Před více než 4000 lety při stavbách egyptských chrámů a pyramid vtipně a jednoduše vytyčovali pravý úhel napínači lan.

Na provaze uvázali 13 uzlů stejně vzdálených od sebe. První uzel spojili s třináctým a provaz napnuli do trojúhelníku se stranami 3, 4, a 5 dílů.


Z obrázku je zřejmé, že pravý úhel leží proti nejdelší straně.

nahoru